Modal decomposition of ECMWF deterministic forecasts

 

Energy spectra

Distribution of atmospheric balanced and inertia-gravity energy as a function of the zonal wavenumber
 

Circulation maps

Regional circulation maps at 850 hPa and 200 hPa
 

Tropical winds

Tropical zonal winds associated with balanced and unbalanced circulation
 

Kelvin waves

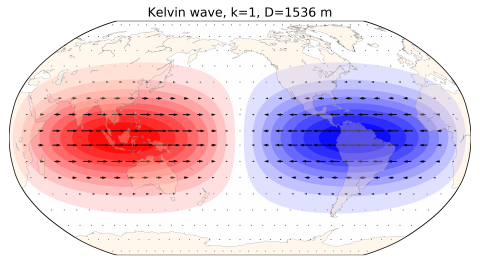
Kelvin waves in the ECMWF model
 

Mixed Rossby-gravity waves

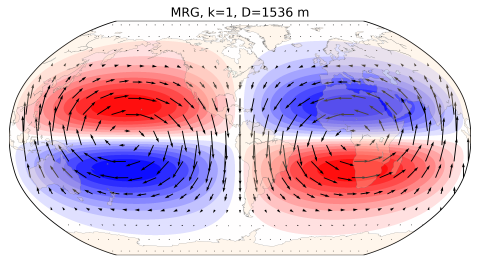
Mixed Rossby-gravity waves in the ECMWF model
 

Polar maps

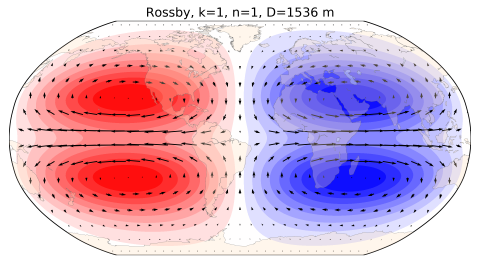
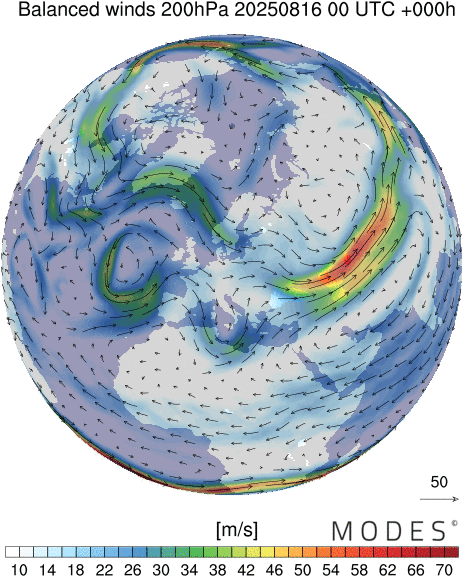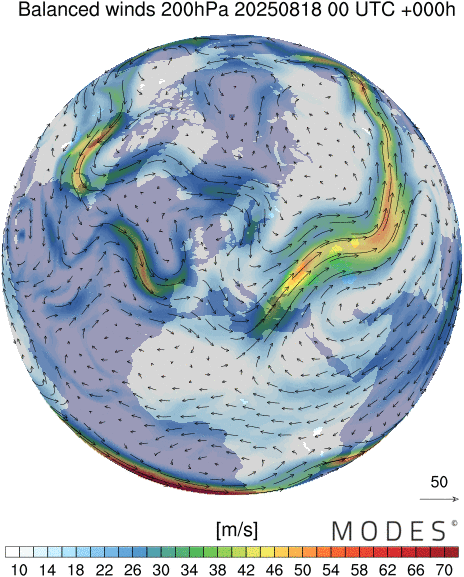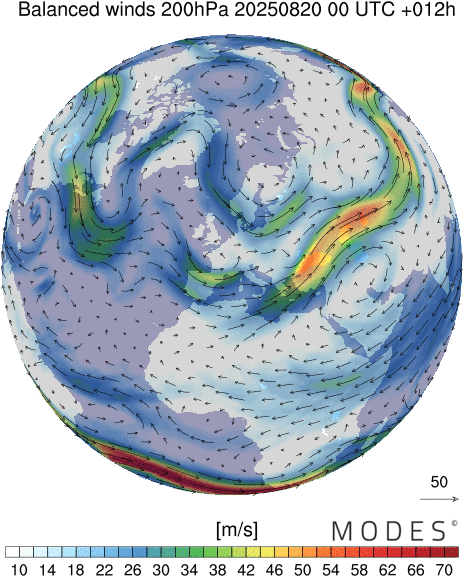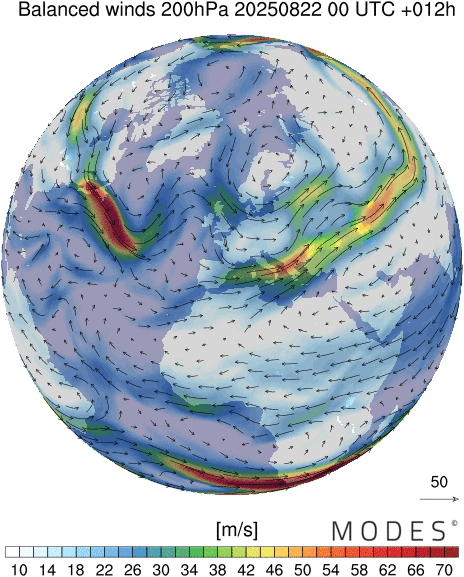
Polar view of midlatitude circulation in the stratosphere
 

n=1 Rossby waves

n=1 Rossby wave horizontal winds and geopotential height (60°S-60°N)
 

Hovmoeller diagrams

Ten-day evolution of the tropical winds on selected levels
 

Inertia-gravity waves

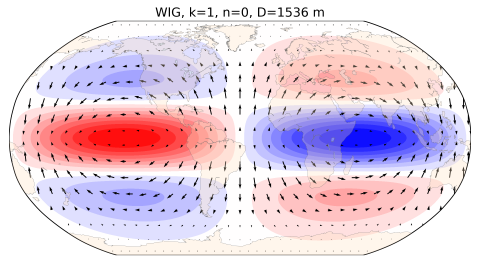
Horizontal winds and geopotential height perturbations associated with eastward and westward inertia-gravity waves (40°S-40°N)

Modal view of atmospheric circulation

representation of the atmosphere

MODES applies three-dimensional linear wave theory for the decomposition of global circulation in terms of normal-mode functions (NMFs). For details, see https://gmd.copernicus.org/articles/8/1169/2015/. MODES outputs quantify spatial and temporal variability associated with the two main circulation regimes, the Rossby wave (or balanced) regime and the inertia-gravity wave (or unbalanced) regime. The approach is most useful in the tropics where the two special NMF solutions, the Kelvin wave and the mixed Rossby-gravity wave, account for a significant part of tropical variability. Recently published book describes theory and applications of normal-mode functions in weather and climate dynamics and numerical weather prediction research: https://www.springer.com/gp/book/9783030609627. MODES pages provide real-time and archive results of modal decomposition of the operational deterministic ECMWF 10-day forecasts. Selected outputs of modal analysis of reanalysis and interesting datasets are also here. A selection of modally filtered climatologies of ERA40 reanalyses are presented in our atlas page.

MODES is maintained and further developed by the Atmospheric Dynamics and Predictability group of Prof. Nedjeljka Žagar at the University of Hamburg.